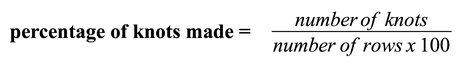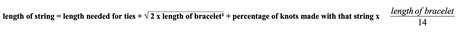Rate Tutorial
Materials needed:
• a normal pattern
• something to calculate
• something to write things down
• something to calculate
• something to write things down
In this tutorial I will introduce you to a formula that allows you to calculate the length of individual strings in a normal pattern. The formula works for bracelets of 14cm length and ties on both ends, but can be adapted to different lengths. I will give you the full formula at the very end.
I use about 10cm of string for the ties per side. If you want longer ties, just add a few extra cm. You also need to add some extra, if you want to make a shaped start or a knotted loop. The calculations don't consider this.
Formula for 14cm bracelet with ties on both ends:
length of string = 45cm + percentage of knots made with that string
I use about 10cm of string for the ties per side. If you want longer ties, just add a few extra cm. You also need to add some extra, if you want to make a shaped start or a knotted loop. The calculations don't consider this.
Formula for 14cm bracelet with ties on both ends:
length of string = 45cm + percentage of knots made with that string
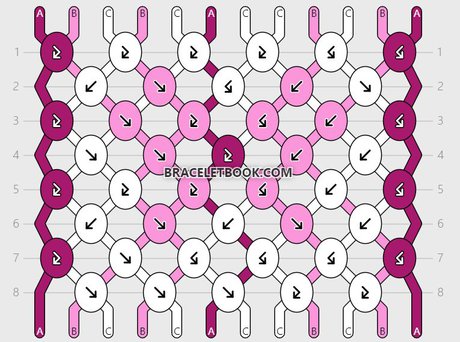
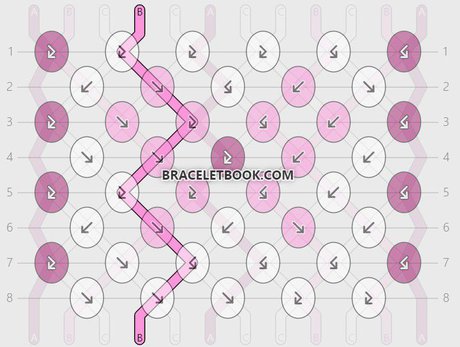
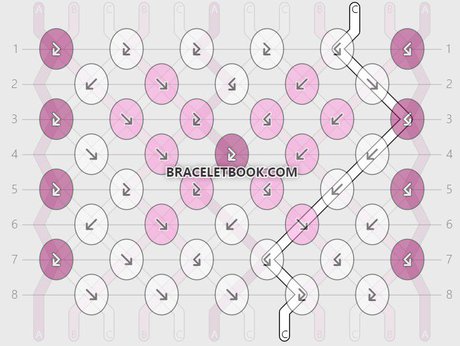
The pattern I will use to explain the formula is pattern #148888 by @dani-robin.
🔸 How to figure out the percentage of knots made with a string?
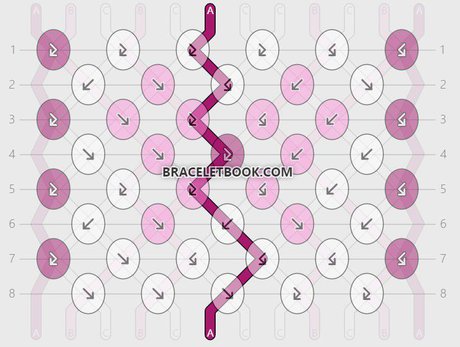
You need to calculate the length for each individual string. To not get confused or accidentally skip strings, I recommend working from left to right when calculating the string length. Start with the left most string. I'm going to call it string 1.
To figure out the percentage of knots made with that string, you need to follow this string from the beginning until the end. On the braceletbook website you can click on the beginning of a string to highlight it. This can be helpful when following the string.
When following the string, there can be two different cases: either the string ends at the same position than it started or it doesn't.
Let's start with the first case.
You need to calculate the length for each individual string. To not get confused or accidentally skip strings, I recommend working from left to right when calculating the string length. Start with the left most string. I'm going to call it string 1.
To figure out the percentage of knots made with that string, you need to follow this string from the beginning until the end. On the braceletbook website you can click on the beginning of a string to highlight it. This can be helpful when following the string.
When following the string, there can be two different cases: either the string ends at the same position than it started or it doesn't.
Let's start with the first case.
🔸 How to figure out the percentage of knots made with a string, if it ends in its starting position?
Follow the string and count all the knots that this string makes onto other strings (where it behaves like the leading string would in an alpha pattern). Divide this number by the amount of rows in the pattern and multiply it by 100.
percentage of knots made = number of knots : (number of rows x 100)
Follow the string and count all the knots that this string makes onto other strings (where it behaves like the leading string would in an alpha pattern). Divide this number by the amount of rows in the pattern and multiply it by 100.
percentage of knots made = number of knots : (number of rows x 100)
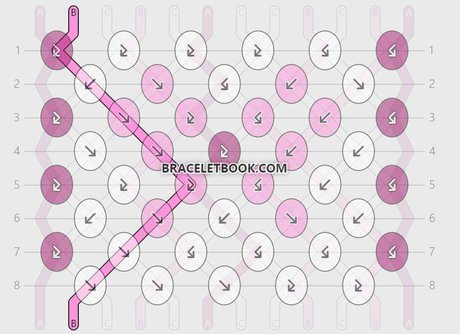
String 1 and string 12:
String 1 ends at the same position it started on. It makes 4 knots. The pattern has 8 rows.
Percentage of knots made with string 1 = 4/8 x 100 = 0,5 x 100 = 50%
Length of string 1 = 45cm + 50% = 95cm
Percentage of knots made with string 1 = 4/8 x 100 = 0,5 x 100 = 50%
Length of string 1 = 45cm + 50% = 95cm
String 2:
String 2 ends at the same position it started on. It makes 3 knots. The pattern has 8 rows.
Percentage of knots made with string 2 = 3/8 x 100 = 0,375 x 100 = 37,5%
Length of string 2 = 45cm + 37,5% = 82,5cm
Percentage of knots made with string 2 = 3/8 x 100 = 0,375 x 100 = 37,5%
Length of string 2 = 45cm + 37,5% = 82,5cm
String 3:
String 3 ends at the same position it started on. It makes 6 knots. The pattern has 8 rows.
Percentage of knots made with string 3 = 6/8 x 100 = 0,75 x 100 = 75%
Length of string 3 = 45cm + 75% = 120cm
Percentage of knots made with string 3 = 6/8 x 100 = 0,75 x 100 = 75%
Length of string 3 = 45cm + 75% = 120cm
String 4:
String 4 ends at the same position it started on. It makes 3 knots. The pattern has 8 rows.
Percentage of knots made with string 4 = 3/8 x 100 = 0,375 x 100 = 37,5%
Length of string 4 = 45cm + 37,5% = 82,5cm
Percentage of knots made with string 4 = 3/8 x 100 = 0,375 x 100 = 37,5%
Length of string 4 = 45cm + 37,5% = 82,5cm
String 5:
String 5 ends at the same position it started on. It makes 3 knots. The pattern has 8 rows.
Percentage of knots made with string 5 = 3/8 x 100 = 0,375 x 100 = 37,5%
Length of string 5 = 45cm + 37,5% = 82,5cm
Percentage of knots made with string 5 = 3/8 x 100 = 0,375 x 100 = 37,5%
Length of string 5 = 45cm + 37,5% = 82,5cm
String 6:
String 6 ends at the same position it started on. It makes 1 knots. The pattern has 8 rows.
Percentage of knots made with string 6 = 1/8 x 100 = 0,125 x 100 = 12,5%
Length of string 6 = 45cm + 12,5% = 57,5cm
Percentage of knots made with string 6 = 1/8 x 100 = 0,125 x 100 = 12,5%
Length of string 6 = 45cm + 12,5% = 57,5cm
String 7:
String 7 ends at the same position it started on. It makes 5 knots. The pattern has 8 rows.
Percentage of knots made with string 7 = 5/8 x 100 = 0,625 x 100 = 62,5%
Length of string 6 = 45cm + 62,5% = 107,5cm
Percentage of knots made with string 7 = 5/8 x 100 = 0,625 x 100 = 62,5%
Length of string 6 = 45cm + 62,5% = 107,5cm
🔸 How to figure out the percentage of knots made with a string, if it doesn't end in its starting position?
If the string does not end in the position it started, you have to follow it until it is in the position again where it started. That means, you have to follow the string during several repeats of the pattern.
If the string starts in position 8, but ends in position 10, you first have to follow it from position 8 until the last row and then from position 10 until the last row. If the string then ends in position 8 again, you can stop following the string, but if it ends in another position, you have to continue following it.
Count all the knots the string makes onto other strings (where it behaves like the leading string would in an alpha pattern) until the string is in the original position again at the end of the pattern. Then you divide the number of knots by the amount of rows it took the string to get to the original position again. The amount of rows is the amount of rows in the pattern multiplied by however many repeats it took until the string was in its original position again.
The percentage you calculated applies for all the starting positions of the string, so in this example, both string 8 and string 10 have the same percentage and therefore the same length.
percentage of knots made = number of knots : (number of rows x 100)
If the string does not end in the position it started, you have to follow it until it is in the position again where it started. That means, you have to follow the string during several repeats of the pattern.
If the string starts in position 8, but ends in position 10, you first have to follow it from position 8 until the last row and then from position 10 until the last row. If the string then ends in position 8 again, you can stop following the string, but if it ends in another position, you have to continue following it.
Count all the knots the string makes onto other strings (where it behaves like the leading string would in an alpha pattern) until the string is in the original position again at the end of the pattern. Then you divide the number of knots by the amount of rows it took the string to get to the original position again. The amount of rows is the amount of rows in the pattern multiplied by however many repeats it took until the string was in its original position again.
The percentage you calculated applies for all the starting positions of the string, so in this example, both string 8 and string 10 have the same percentage and therefore the same length.
percentage of knots made = number of knots : (number of rows x 100)
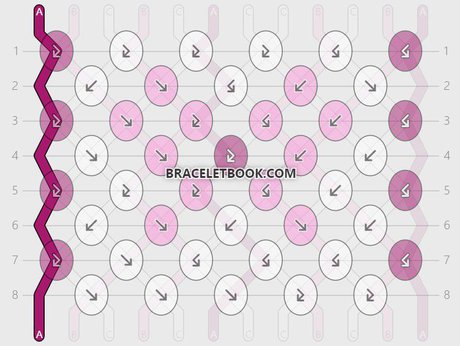
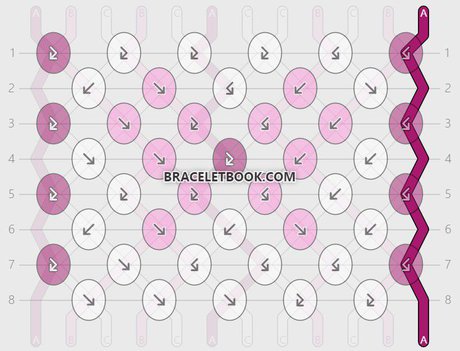
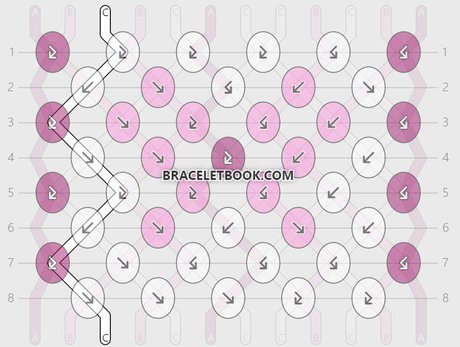
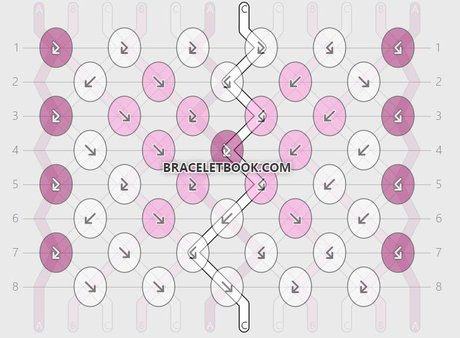
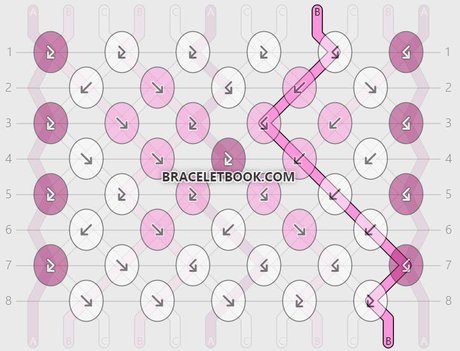
String 8 and string 10:
String 8 ends in position 10. String 10 ends in position 8. String 8 and string 10 make 9 knots. It takes 2 repeats (16 rows) until they are in the original position again.
Percentage of knots made with strings 8 and 10 = 9/16 x 100 = 0,5625 x 100 = 56,25 %
Length of strings 8 and 10 = 45cm + 56,25% = 101,25 cm
Length of strings 8 and 10 = 45cm + 56,25% = 101,25 cm
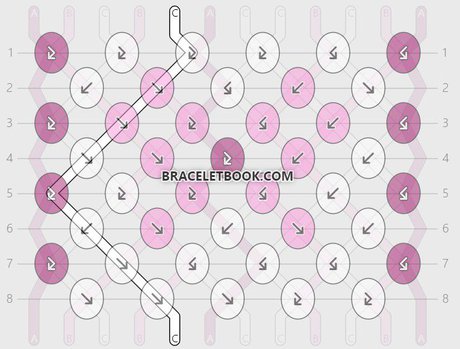
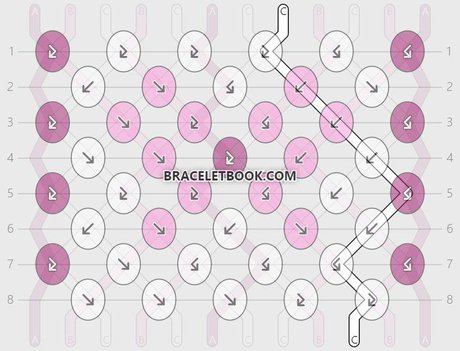
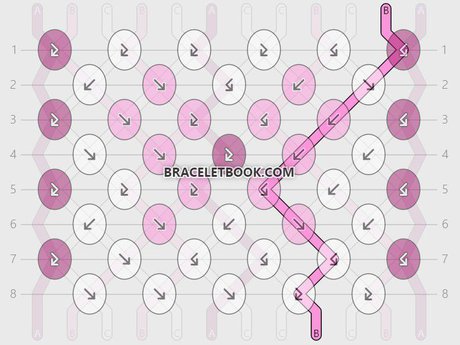
String 9 and string 11:
String 9 ends in position 11. String 11 ends in position 9. String 9 and string 11 make 6 knots. It takes 2 repeats (16 rows) until they are in the original position again.
Percentage of knots made with strings 9 and 11 = 6/16 x 100 = 0,375 x 100 = 37,5%
Length of strings 9 and 11 = 45cm + 37,5% = 82,5cm
Length of strings 9 and 11 = 45cm + 37,5% = 82,5cm
Overview over the string length needed
In this pattern:
• 2 strings of colour A for the borders: 95cm
• 1 string of colour A for the body of the butterfly: 57,5cm
• 4 strings of colour B for the wings of the butterfly: 82,5cm
• 1 string of colour C (string 3): 120cm
• 1 string of colour C (string 5): 82,5cm
• 1 string of colour C (string 7): 107,5cm
• 2 strings of colour C (strings 8 and 10): 101,5cm
You can see that some strings of the same colour need different length. For this formula to work out, you have to make sure, that you place all the strings in the correct position. You also have to follow the pattern exactly. Even if there is a knot between two strings of the same colour, you have to make the knot the pattern tells you to make. Otherwise the calculation won't be accurate any more.
• 2 strings of colour A for the borders: 95cm
• 1 string of colour A for the body of the butterfly: 57,5cm
• 4 strings of colour B for the wings of the butterfly: 82,5cm
• 1 string of colour C (string 3): 120cm
• 1 string of colour C (string 5): 82,5cm
• 1 string of colour C (string 7): 107,5cm
• 2 strings of colour C (strings 8 and 10): 101,5cm
You can see that some strings of the same colour need different length. For this formula to work out, you have to make sure, that you place all the strings in the correct position. You also have to follow the pattern exactly. Even if there is a knot between two strings of the same colour, you have to make the knot the pattern tells you to make. Otherwise the calculation won't be accurate any more.
How well does it work?
Even when calculating the string length, you will still most likely have some string left over. When I tied this bracelet, there was left-over for all of the strings, but all the left-over was between 10cm and 20cm long. If I had just cut all strings the same length and extra long just to be save, I would have had a lot more left over.
🔸 How to adapt the formula to different bracelet and tie length?
What comes next is going to be a little more complicated, but no worries, you can stop reading at this point. The following is not essential for this tutorial. It is only meant for those who want to adapt the formula and those of you who are interested in the mathematics behind this formula and how it was made. I want to apologise in advance for my formula not meeting mathematical standards 😉
I promised to give you the adaptable formula in the end and here it is:
length of string = length needed for ties + square root of (2 x (length of bracelet^2)) + percentage of knots made with that string x (length of bracelet/14)
What comes next is going to be a little more complicated, but no worries, you can stop reading at this point. The following is not essential for this tutorial. It is only meant for those who want to adapt the formula and those of you who are interested in the mathematics behind this formula and how it was made. I want to apologise in advance for my formula not meeting mathematical standards 😉
I promised to give you the adaptable formula in the end and here it is:
length of string = length needed for ties + square root of (2 x (length of bracelet^2)) + percentage of knots made with that string x (length of bracelet/14)
Explanation of the formula:
Looking at this is probably a little confusing, so I am going to explain this formula using the numbers inserted for the 14cm bracelet.
Length needed for the ties
The length I use per tie is about 10cm. So I add 20cm for ties on both ends.
square root of (2 x (length of bracelet^2))
This square root is what you would need for a string, if it made 0% knots.
You're probably wondering why that is. Strings in normal patterns move at a diagonal of about 45° . The way you can calculate how long this diagonal is, is by using the Pythagorean theorem. If you have a triangle with a right angle, a square that has the side length of the hypotenuse c (the side opposite the right angle) has the same area as the area of the squares on the other two sides a and b.
This can be written down as the equation a2 + b2 = c2. Which means that c = sqrt(a2 + b2).
We want to know c. In our case the two sides a and b are about 14cm long.
c2 = 142+ 142 = 392
c = sqrt(392) ≈ 19,8
Length needed for the ties
The length I use per tie is about 10cm. So I add 20cm for ties on both ends.
square root of (2 x (length of bracelet^2))
This square root is what you would need for a string, if it made 0% knots.
You're probably wondering why that is. Strings in normal patterns move at a diagonal of about 45° . The way you can calculate how long this diagonal is, is by using the Pythagorean theorem. If you have a triangle with a right angle, a square that has the side length of the hypotenuse c (the side opposite the right angle) has the same area as the area of the squares on the other two sides a and b.
This can be written down as the equation a2 + b2 = c2. Which means that c = sqrt(a2 + b2).
We want to know c. In our case the two sides a and b are about 14cm long.
c2 = 142+ 142 = 392
c = sqrt(392) ≈ 19,8
Why 45cm and not 39,8cm as the base length?
You might be wondering, why I then use 45cm and not 20cm + 19,8cm = 39,8cm as the length where I add the rest of the length to. The extra 5cm are just there for added security and have no mathematical explanation.
Why the percentage?
Now why the percentage? When I was trying to come up with this formula, I was sure, that what mattered was the ratio of knots a string makes. The more knots a string makes, the more string is needed. The less knots a string makes, the less string is needed.
I tied some test bracelets and measured the amount of strings I used for those. It turned out that for a 14cm long bracelet, the percentage of knots made equalled exactly the amount of cm I needed to add to the base length. This was a lucky coincidence. For any other length the exact percentage would not have worked out. To still be able to work with the percentage, you just have to multiply it by the bracelet length you want divided by 14.
I tied some test bracelets and measured the amount of strings I used for those. It turned out that for a 14cm long bracelet, the percentage of knots made equalled exactly the amount of cm I needed to add to the base length. This was a lucky coincidence. For any other length the exact percentage would not have worked out. To still be able to work with the percentage, you just have to multiply it by the bracelet length you want divided by 14.